The definition of Accumulated Cyclone Energy does not make sense.
Definition of Accumulated Cyclone Energy ##
as lifted from wikipedias entry:
“The ACE of a season is calculated by summing the squares of the estimated maximum sustained velocity of every active tropical storm (wind speed 35 knots (65 km/h) or higher), at six-hour intervals. If any storms of a season happen to cross years, the storm’s ACE counts for the previous year. The numbers are usually divided by 10,000 to make them more manageable. The unit of ACE is 104kt2, and for use as an index the unit is assumed.”
But those units don’t match the definition and cannot be right. -even if that is how everybody reports ACE. It is an integrated squared velocity over time, summed over all storms. The units are $speed^2 \cdot time$. You can get rid of the “time” by reporting the ACE per year rather than the pure ACE and then you will get $speed^2 \cdot time / time$. But that only cancels out if the nominator and denominator are in the same units of time. The number of 6hour blocks per year is 1461.
An example:
The Atlantic 2005 season is commonly reported to have an ACE of ~250e4 kt2. That is wrong! If we want to report in kt2 units and take into account that there are 1461 timesteps/year then we get: ACE/yr=1711 kt2. I am not a fan of this way of reporting it either. But it illustrates that the definition of ACE is sloppy.
Energy is a misnomer
The idea that cyclone energy is proportional to v2 is also poorly justified. The energy of what exactly are we talking about?
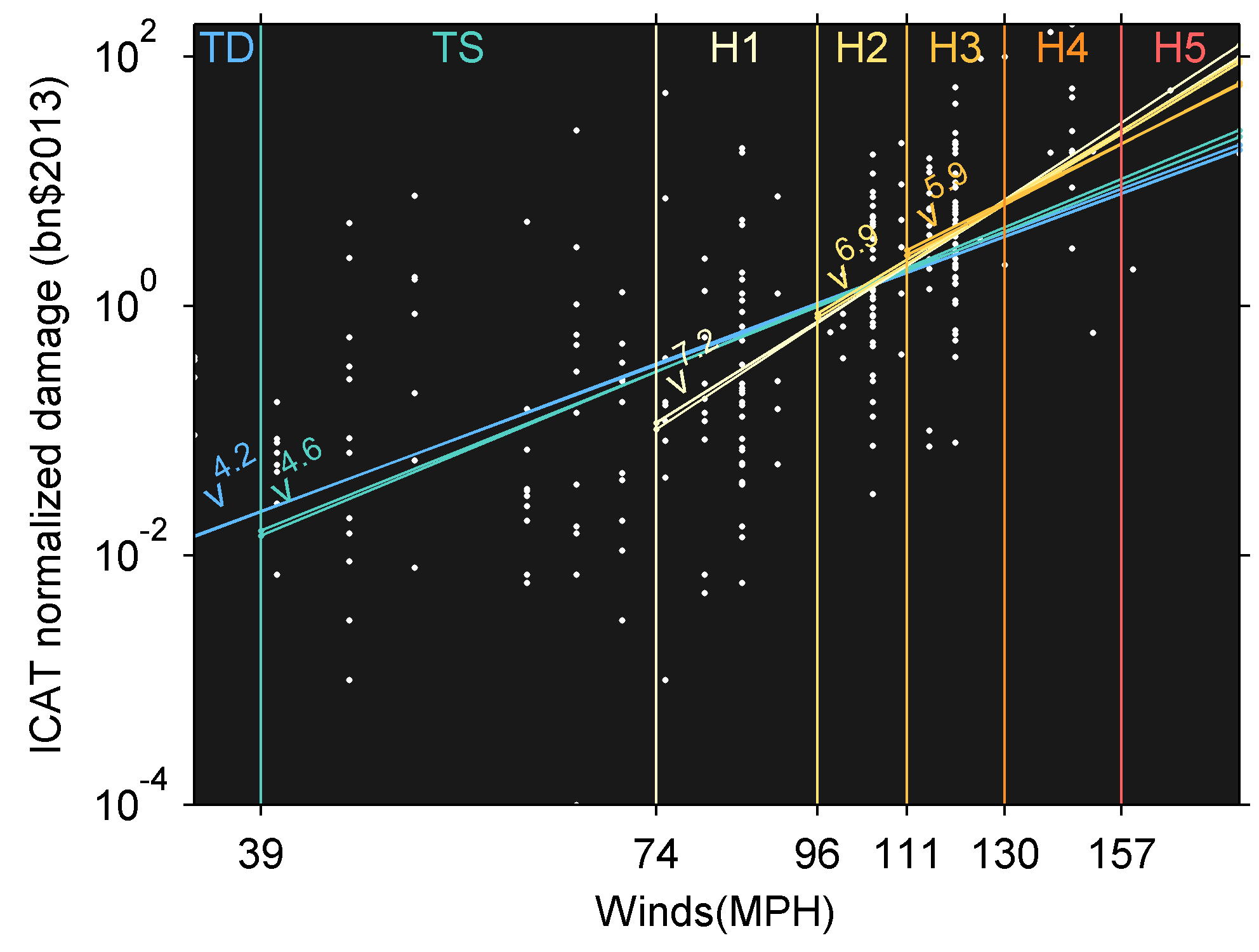
The “Energy” in ACE is a misnomer. I am not alone in thinking this but it should be testable in GCMs (scatterplot of some well defined measure of cyclone energy vs ACE). I believe that ACE is simply some index which is useful because it is easy to calculate, and allows comparison with earlier work. So while it may be practical for some purposes then the theoretical justification is weak. I guess it is good that it is non-linear in v and that it takes duration into account. This is important for risk/potential damage. Potential damage would require a greater exponent though (perhaps something like v6.5see figure). In the figure below I plot loglog fits. Murnane et al. 2012 find that another type of law give better fits $$ Dmg \propto \exp^{aV} $$. This type of law is able to capture the curvature evident from the lower slopes at low wind speeds.
The end… I cannot be bothered wasting more time with this rant.
Is ACE better than named storm counts?
That depends… Big storms definitely pose a more severe threat so if you want to rank the severity of different seasons, then ACE is better than storm count. But you could look at hurricane damage instead or at something like $ wind^6 $ (see below).
However, if you want to try to understand how climate change affect the risk then it may be better to look at frequencies. At least if your mental model is one where frequencies are changing. E.g. if you are assuming some stochastic process where:
- P(damage|maxwind,exposure) is stationary
- P(maxwind|storm) is stationary
- P(storm) time-varying (due to AGW / ENSO /… )
Here, expected hurricane losses per year scales linearly with frequency because all else is being equal. In this case it is clearly better to look at frequencies if you want to estimate how expected annual damage changes with time. My point is that what is best depends on your expectations for how the world is put together. (I am not arguing for this particular mental model). Frequency measures are obviously best at detecting changes in frequency.
Finally, I think that if you are building models to detect the trends etc. then I think you will get much more out of the data if you do not aggregate the data into a single number per season. This amounts to discarding information. It is useful for presentation and simple analysis like straight line fits, but you will get better results if you try to model it in more detail.
