Ritz et al. (2015) have a recent model study of potential sea level rise from Antarctic marine ice sheet instability.
In it they conclude:
“Our assessment suggests that upper-bound estimates from low-resolution models and physical arguments (up to a metre by 2100 and around one and a half by 2200) are implausible under current understanding of physical mechanisms and potential triggers”.
I like the study, -yet I am not ready to accept their assessment that higher rates are implausible. There are several reasons for this, but the most important is that this is a single study, and while they do a commendable job in exploring uncertainties, then history is littered with examples of overconfidence. See for example these estimates of the speed of light over time, where estimates clearly have had too narrow confidence intervals (from “Ubiquitous Overconfidence” section in Morgan et al., 2014):
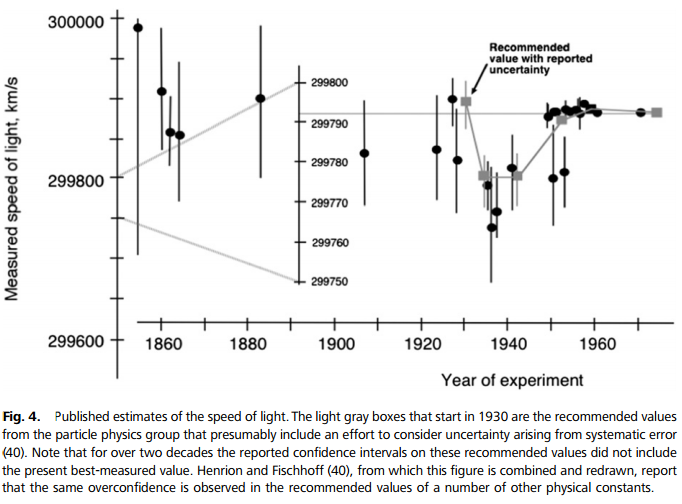
The Ritz et al. modelling approach is to some extent conditional on our physical understanding, and new mechanisms have been proposed which make the ice sheet respond an order of magnitude faster (Pollard et al., 2015). For that reason alone I think it is too early to say “implausible”. Ritz et al. do acknowledge the possibility of new physics in their final sentence:
But, given current understanding, our results indicate that plausible predictions of Antarctic ice-sheet instability leading to greater than around half a metre of sea-level rise by 2100 or twice that by 2200 would require new physical mechanisms23, new projections of MISI triggers, or both.
You can look at this problem from many perspectives: modelling, paleo evidence, semi-empirical, and people do. Different experts will assign different weights to different lines of evidence. I think the best (and probably most objective) way to quantify the broader uncertainty is through formal expert elicitations such as Bamber & Aspinall (2013). Maybe expert opinion have moved since BA13, -and I hope that an updated formal elicitation will come out soon. There have been several new studies since BA13 suggesting that WAIS (in particular the ASE region) may already be committed to collapse. On the other hand, we have also had a range of model studies concluding that it probably would not happen that fast. But, then we also have Pollard et al. which highlights a mechanism that potentially could make it go a lot faster. The case for a WAIS collapse during the last interglacial has strengthened the last few years in my opinion. So, in my view it is not trivial to conclude how the full uncertainty has evolved. -and that is why we need a new elicitation.
Note: this was written in a rush. Please, excuse any trailing thoughts and unfinished sentences.
Updates
Update: DeConto & Pollard have published projections where they include the new processes they found were necessary to include . Where Ritz et al. finds a metre or more to be implausible, DeConto & Pollard finds that not only plausible but even likely (for RCP8.5). Their 95th percentile is at ~1.5m and their median estimate is ~0.7m for RCP8.5. That is substantially higher than Bamber & Aspinall (2013).
Update: Greg Laden has a nice exchange on the subject between Richard Alley (from the Pollard et al. Study) and Tamsin Edwards (of the Ritz et al. study). Great to hear their own views. Go and read for yourself.
Observe how the 83% interval of BA13, is reasonably similar to 95% of other studies. I note that in AR5 they concluded that the full uncertainty is greater than ensemble spread alone for several key quantities (e.g. steric expansion). They therefore inflated model-spread by a factor 2, which essentially maps 95% model spread to 83% uncertainty intervals.
Update: I think the difficulty with defining an upper limit for the AIS contribution to SLR is similar to the difficulty with assigning an upper limit to climate sensitivity. Here’s a figure from AR4 (chosen because it is plotted as a CDF). I think this figure makes it easy to appreciate why model spread alone (green) does not capture the full uncertainty.
Edit: Fixed a few inverted statements. Thanks to @p_aulina
